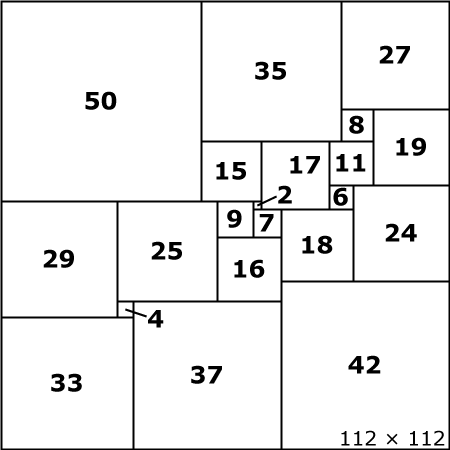
Wieder was gelernt: Das „perfekt quadrierte Quadrat“ besteht also mindestens 21 kleineren Quadraten unterschiedlicher Größe, die das große Quadrat lückenlos füllen, und Roland Sprague hat das 1939 zuerst herausgefunden. Er war Mathematiker, vielleicht aber auch Tischler. Oder beides. Bob Mackay hat schließlich auch ein Faible für Zahlen und Schränke und hat ganz viele quadratische Schubladen (nun ja, 21 eben) gebaut, die ich allerdings noch etwas unsexier finde als die obige Zeichnung, weshalb ich mich für jene als Illustration dieses spannenden Artikels entschieden habe.
Die Website zu diesem hochinteressanten Hobby heißt squaring.net, und ich weiß das nur, weil’s bei Make steht.
Ist vielleicht für irgendeinen besoffenen Abend in der Kneipe mal ganz gut. Über sowas zerbrechen ja gerne mal Freundschaften.
UPDATE Ursprünglich hatte ich geschrieben, man könne ein Quadrat in höchstens 21 unterschiedlich große kleinere Quadrate lückenlos unterteilen, das war Blödsinn, wie mehrere Leser in den Kommentaren zurecht feststellten. Man braucht also mindestens 21 Stück, darunter hat es noch niemand geschafft.







„Quatsch, wenn ich ein Quadrat mit einer Kantenlänge von 1.000.000 habe, und dann mit einem Quadrat mit einer Kantenlänge von 1 anfange, dann mit 2 usw… ach warte mal, die müssen ja auch noch ineinander passen, uff, dann geht das mit dem 1er ja wohl nicht. Hm…. stimmt wohl“
(Schon komisch, dass man gerade über sowas dann doch ein paar Minuten nachdenkt…)
hä – man kann dann doch jedes dieser 21 quadrate in sich wieder unterteilen, oder habe ich was nicht verstanden?
Da es das Triangulieren gibt, also auch das Quadrieren. In manchen Situationen reduziert sich alles darauf: http://gedichtbandlose-lyrik.de/keine-loesung
@#789033: Das verstehe ich auch nicht. Vielleicht ist es auch noch abhängig von der Größe, wenn man bei ganzen Einheiten bleibt. Das 50er Quadrat lässt sich also vielleicht nicht genau quadrieren? Vielleicht ist die 112er-Einheit eine der wenigen?
Vermutungen sind in der Mathematik wenig hilfreich, ich weiß. :)
Die verschiedenen Größen dürfen ja trotzdem nicht doppelt vorkommen. ;)
Hoi, also die Formulierung ist nicht ganz so gut gewählt. Man kann ein Quadrat natürlich in mehr als 21 kleinere, unterschiedliche Quadrate zerteilen. Die Sache ist die, dass man MINDESTENS 21 kleinere Quadrate braucht.
Und @munk: Es müssen aber unterschiedliche Quadrate sein…
Grüße!
„Man kann ein Quadrat höchstens in 21 kleinere Quadrate unterschiedlicher Größe unterteilen.“
Da hast du wohl etwas falsch verstanden Johnny. Das kleinste perfekt quadrierte Quadrat besteht aus 21 Quadraten. Es gibt aber durchaus perfekt quadrierte Quadrate höherer Ordnung (http://www.squaring.net/sq/ss/spss/o31+/SPSSo31-75.pdf). Richtig müsste es heißen:
Will man ein Quadrat in kleinere Quadrate unterschiedlicher Größe aufteilen, so braucht man mindestens 21.
Edit: Sylvus war wohl schneller
Roland Sprague (1894 – 1967) war ein deutscher Mathematiker. Er hat 1950 an der Freien Universität Berlin promoviert. Ob er auch Tischler war, weiß ich nicht.
Und was wenn ich es in 44 Quadrate unterteile? Wieso 21?
Ich kann bei den Schubladen nur 20 Stück sehen. Das ist vermutlich mathematische Blindheit oder „die Augen vor der hohen Mathematik verschließen“.
noch kurz nacherklärt: mir war schon klar, dass es unterschiedlich große sein sollen. aber man kann dann zum beispiel das allerkleinste der 21 quadrate nehmen und das wiederum in 21 unterquadrate teilen, diese neuen 21 quadrate sind alle wieder anders groß als alle bisherigen.
@#789037: @#789038: Ah. Das erklärt einiges. Wieso kam ich auf „höchstens“?? Wird sofort korrigiert, danke sehr!
Yo dawg, we heard you like squares, so we put a square in your squa…. okay ich hör schon auf.
Triangulieren und Quadrieren ist ja ganz interessant, aber der oberhammer bleibt doch das palindromisieren von zahlen (und die entstehenden grafiken).
>mindestens 21 Stück … (UPDATE)
www squaring net / sq / tws.html
da sind nur elf!
@#789091: Ist ein Rechteck.
Um die Geschichte von quadrierten Quadraten zu korrigieren: Sprague hat 1939/1940 eine Zerlegung eines Quadrates in 55 Quadrate veröffentlicht. Diese beruht auf geschicktem Aneinanderlegen von damals bereits bekannten quadrierten Rechtecken und ist demnach nicht compound – enthält also mindestens ein Rechteck, welches bereits lückenlos durch Quadrate bedeckt wird. Damit hat er als erster Mathematiker die Existenz solch einer Zerlegung gezeigt, welche vorher durch Lousin angezweifelt wurde.
1940 haben Brooks, Smith, Stone und Tutte die Theorie für quadrierbare Rechtecke in der Arbeit „The dissection of rectangles into squares“ geschaffen, die im wesentlich auf Netzwerktechnik basiert und die Kirchhoffschen Gesetze in planaren Graphen anwendet. Dadurch haben sie eine Zerlegung eines Quadrates in 26 unterschiedlich große Quadrate entdeckt.
Die oben gezeigt Zerlegung in 21 Quadrate wurde vom Holländer Duijvestijn 1962 mit Hilfe von Computern gefunden, indem jedes planare Netzwerk mit bis zu 22 Kanten erstellt und ausgewertet wurde.